Brief Announcement: A Local Stochastic Algorithm for Separation in Heterogeneous Self-Organizing Particle Systems

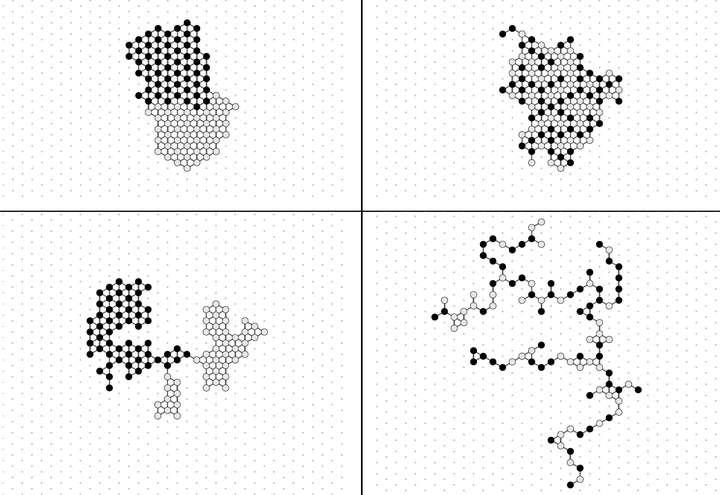
Abstract

We investigate stochastic, distributed algorithms that can accomplish separation and integration behaviors in self-organizing particle systems, an abstraction of programmable matter. These particle systems are composed of individual computational units known as particles that have limited memory, strictly local communication abilities, and modest computational power, and which collectively solve system-wide problems of movement and coordination. In this work, we extend the usual notion of a particle system to treat heterogeneous systems by considering particles of different colors. We present a fully distributed, asynchronous, stochastic algorithm for separation, where the particle system self-organizes into segregated color classes using only local information about each particle’s preference for being near others of the same color. Conversely, by simply changing the particles' preferences, the color classes become well-integrated. We rigorously analyze the convergence of our distributed, stochastic algorithm and prove that under certain conditions separation occurs. We also present simulations demonstrating our algorithm achieves both separation and integration.