Improved Leader Election for Self-Organizing Programmable Matter

Abstract

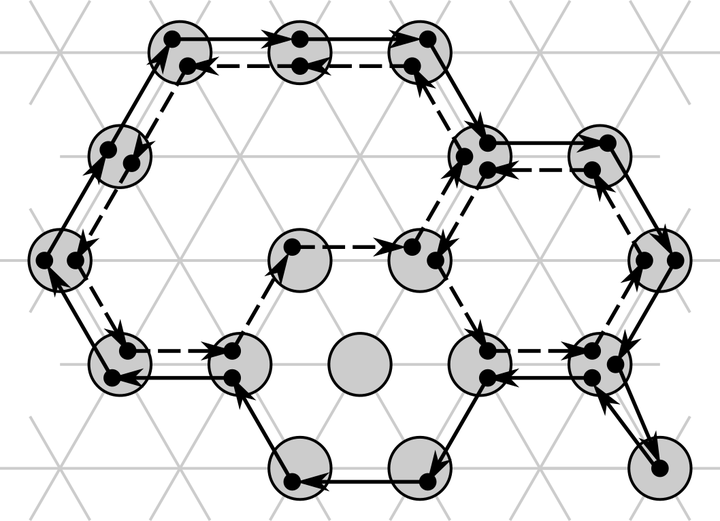
We consider programmable matter that consists of computationally limited devices (called particles) that are able to self-organize in order to achieve some collective goal without the need for central control or external intervention. We use the geometric amoebot model to describe such self-organizing particle systems, which defines how particles can actively move and communicate with one another. In this paper, we present an efficient local-control algorithm which solves the leader election problem in ${\cal O}(n)$ asynchronous rounds with high probability, where $n$ is the number of particles in the system. Our algorithm relies only on local information — particles do not have unique identifiers, any knowledge of $n$, or any sort of global coordinate system — and requires only constant memory per particle.