Deadlock and Noise in Self-Organized Aggregation Without Computation

Abstract

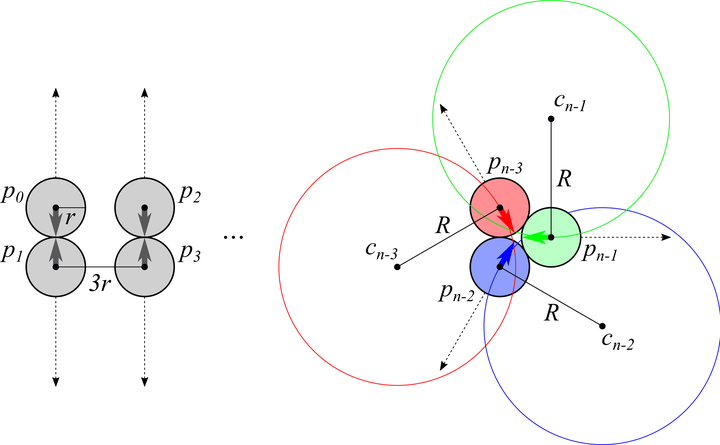
Aggregation is a fundamental behavior for swarm robotics that requires a system to gather together in a compact, connected cluster. In 2014, Gauci et al. proposed a surprising algorithm that reliably achieves swarm aggregation using only a binary line-of-sight sensor and no arithmetic computation or persistent memory. It has been rigorously proven that this algorithm will aggregate one robot to another, but it remained open whether it would always aggregate a system of $n > 2$ robots as was observed in experiments and simulations. We prove that there exist deadlocked configurations from which this algorithm cannot achieve aggregation for $n > 3$ robots when the robots' motion is uniform and deterministic. In practice, however, the physics of collisions and slipping work to the algorithm’s advantage in avoiding deadlock; moreover, we show that the algorithm is robust to small amounts of noise in its sensors and in its motion. Finally, we prove that the algorithm achieves a linear runtime speedup for the $n = 2$ case when using a cone-of-sight sensor instead of a line-of-sight sensor.