Local Mutual Exclusion for Dynamic, Anonymous, Bounded Memory Message Passing Systems

Abstract

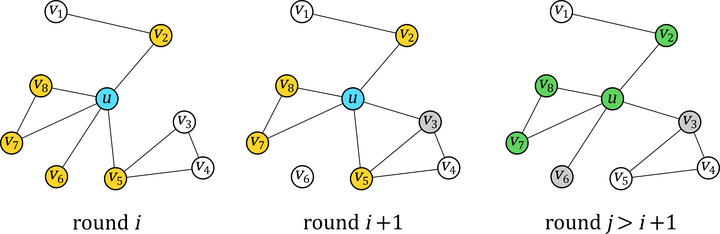
Mutual exclusion is a classical problem in distributed computing that provides isolation among concurrent action executions that may require access to the same shared resources. Inspired by algorithmic research on distributed systems of weakly capable entities whose connections change over time, we address the local mutual exclusion problem that tasks each node with acquiring exclusive locks for itself and the maximal subset of its “persistent” neighbors that remain connected to it over the time interval of the lock request. Using the established time-varying graphs model to capture adversarial topological changes, we propose and rigorously analyze a local mutual exclusion algorithm for nodes that are anonymous and communicate via asynchronous message passing. The algorithm satisfies mutual exclusion (non-intersecting lock sets) and lockout freedom (eventual success with probability 1) under both semi-synchronous and asynchronous concurrency. It requires $\mathcal{O}(\Delta)$ memory per node and messages of size $\Theta(1)$, where $\Delta$ is the maximum number of connections per node. We conclude by describing how our algorithm can implement the pairwise interactions assumed by population protocols and the concurrency control operations assumed by the canonical amoebot model, demonstrating its utility in both passively and actively dynamic distributed systems.